Continuité de surface
Pour faire une modélisation complexe en surfacique il faut séparer en surface simple notre modèle.

Dans cette souris, pour arrivé à faire une forme complexe sans arêtes apparentes il faut diviser la surface en plusieurs surfaces simples. Dans notre exemple, la surface rouge du dessus a été créé en premier ensuite on a fait les 4 côtés (orangé, bleu, violet et rose) en s'assurant de fondre les surfaces ensemble pour que le début et la fin des surfaces soient invisible. On appelle ces surfaces des surfaces tangentes. Ensuite les surfaces qui forme les 4 coins ont été ajouté (jaune, violet et cyan) Encore une fois on a pris soit de faire des surfaces tangentes à la face rouge du dessus mais aussi aux 4 faces de côté faites précédemment. Le résultat est une formes complexe réaliser de 9 surfaces plus simple.
Les types de continuité de surface
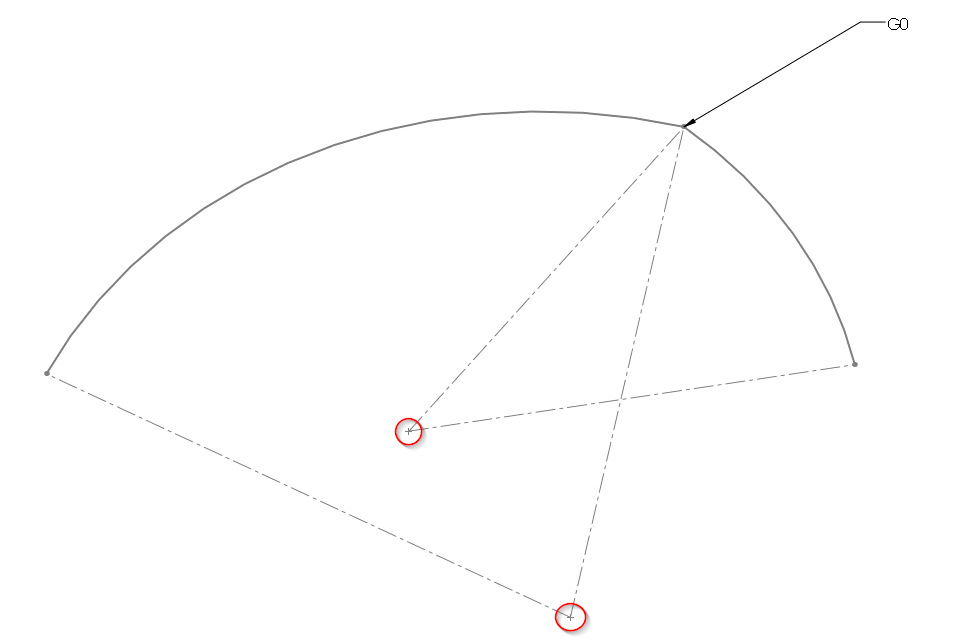
G0 (G-zéro) ou : de position
2 surfaces n'ont que la position de l'arête de similaire. les surfaces ne sont pas aligné. On a donc des arêtes fisible entre les surfaces. Dans cette voiture Hyundai, des lignes de caractères sont visible dans les portières, les surfaces de chaque côté de la ligne sont en G0 (zéro)

Voici une représentation 2d de cette situation. Les 2 courbes ne se touche à un point et leur rayon ne sont pas alignés sur une même ligne.
G1 tangente
On dit de deux surface qu'elle sont tangente quand leur rayon sont aligné sur une même ligne.
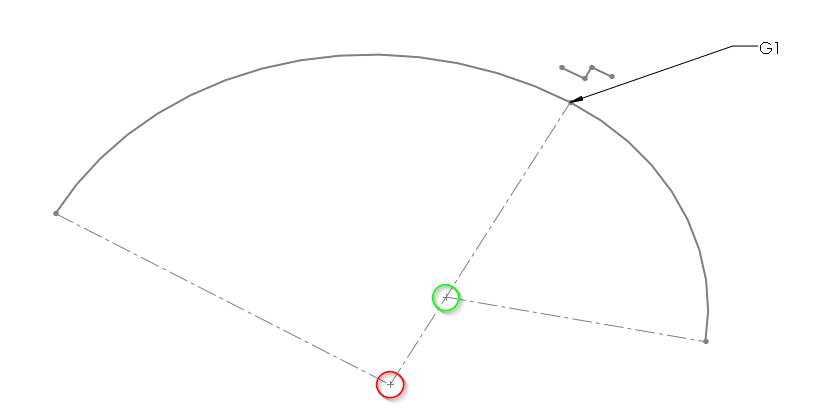
Dans cette illustration, le point rouge représente le centre de la courbe de gauche et les lignes pointillées représente les rayons de la courbe qui relie la courbe à sont centre. Le point vert représente le centre de la courbe de droite. On voit que le centre de la courbe en vert est sur la même ligne que le rayon de la courbe de gauche. Les lignes sont donc tangente.
Notez que les courbes peuvent aussi aller dans des directions inverse et tout de même resté tangentes. dans cette illustration, on voit que les rayons forme une ligne droite d'une courbe à l'autre. Les courbes sont donc tangentes.
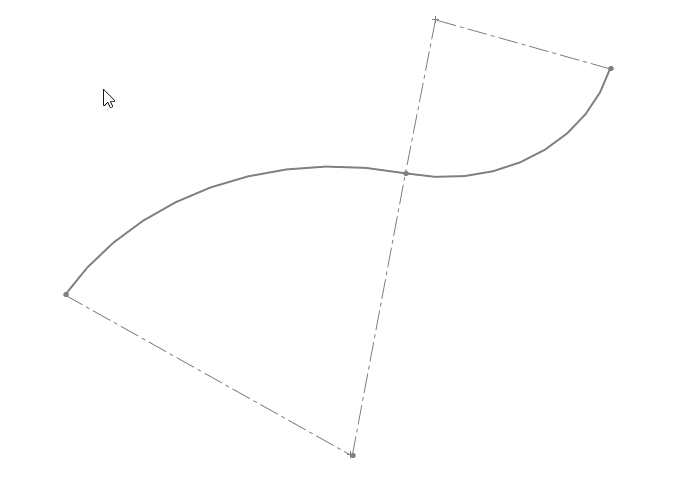
G2 Courbure continue
On dit que la continuité entre deux surfaces est courbure continue quand en plus d'être tangentes, deux surfaces on aussi la même longueur de rayon à leur point de rencontre.
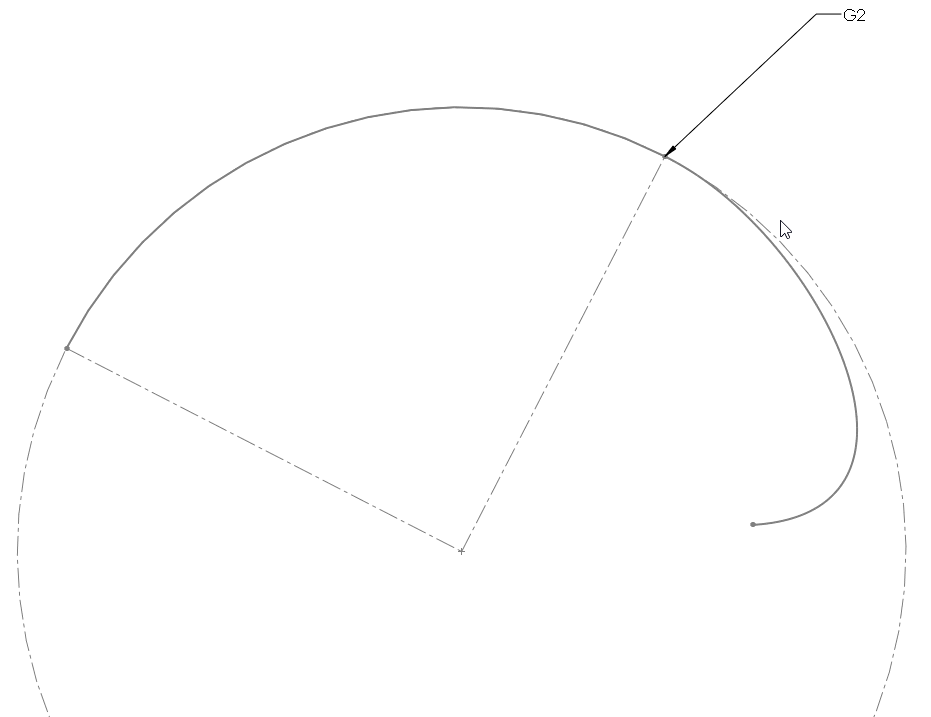
Dans cette illustration on voit que l'arc de cercle à gauche est connecté avec un spline qui au départ à un rayon identique à celui de la courbe de gauche. Ce niveau de continuité créera des surfaces parfaitement continue. La connexion entre les surfaces sera indétectable.